MATEMÁTICAS BÁSICAS
ÁNGULOS Y SISTEMAS DE MEDICIÓN
La siguiente actividad interactiva te permitirá activar tus conceptos previos sobre ángulos y diferentes contextos donde se aplican.
El siguiente vídeo te permite complementar tus conceptos sobre ángulos y sus elementos.
SISTEMA SEXAGESIMAL
El siguiente vídeo te ilustra el cómo convertir un ángulo decimal en grados, minutos y segundos.
El siguiente vídeo te ilustra sobre cómo convertir de grados decimales a grados sexagesimal ( grados, minutos y segundos).
El siguiente vídeo te ilustra sobre cómo convertir el grado en notación sexagesimal ( grados, minutos, segundos ) a grados decimales.
El siguiente vídeo te ilustra sobre como convertir de radianes a grados.
Ejemplo
El siguiente vídeo complementa tu información sobre cómo calcular la longitud de un arco.
El siguiente vídeo te permite complementar tu información sobre el calculo de sector circular.
La siguiente actividad interactiva te facilitará la identificar el tipo de triángulo, el nombre de los lados y además facilita la demostración del teorema de Pitágoras te invito a realizar las actividades interactivas propuesta 1,2 y 3 , y a ganar puntos extra.
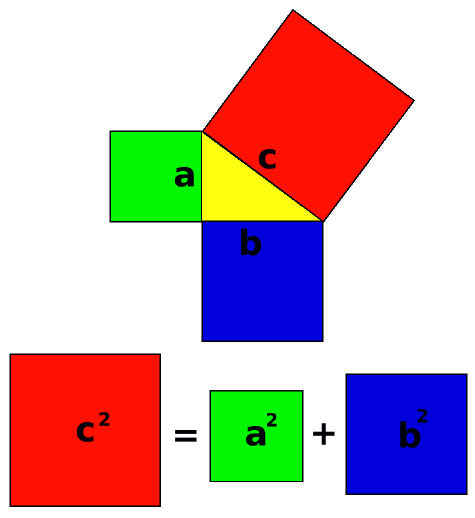
El teorema de Pitágoras es un teorema que se aplica únicamente a Triángulo rectángulo, te invito a observar un vídeo que te ilustra sobre los triángulos rectángulos y hace una introducción al teorema de Pitágoras.
El siguiente Vídeo Te permite complementar la información sobre el teorema de Pitágoras
Las siguientes expresiones permiten conocer la medida de un cateto, conocida la hipotenusa y uno de los catetos.
El siguiente vídeo te ilustra sobre cómo calcular los diferentes lados de un triangulo rectángulo conociendo dos de los tres lados.
- Cálculo de la hipotenusa conocido dos lados.
- Calculo de uno de los catetos conocida la hipotenusa y uno de los catetos.
Calculo de distancia en el plano cartesiano
Para calcular distancias en el plano cartesiano, se identifican las coordenadas de los dos puntos de coordenadas ( X1, Y1) y ( X2, Y2) y se utiliza la siguiente expresión:
El siguiente vídeo te ilustrará sobre el calculo de distancia en el plano cartesiano conocida la coordenada de los puntos.
También se puede simplificar el calculo de la distancia entre los dos puntos conocidas las coordenadas de los dos puntos, se traza la recta entre estos dos puntos , dicha recta conforma la hipotenusa del triangulo rectángulo.
ACTIVIDAD DE PUNTO ADICIONAL.
En el siguiente enlace, encontrarás actividad interactiva, donde aplicarás los conceptos visto relacionados con el teorema de Pitágoras y te colocará a prueba sobre el cálculo del lado desconocido de un triángulo rectángulo conociendo dos de sus lados.
Diviértete aplicando lo aprendido sobre el teorema de Pitágoras resolviendo crucigrama de manera interactiva.
El siguiente crucigrama te permite aprender de manera divertida los conceptos básicos del teorema de Pitágoras.
Los siguientes vídeos te
SOLUCIÓN DE PROBLEMAS CON EL TEOREMA DE PITÁGORAS
VERIFICA LA SOLUCIÓN DE TUS TRIÁNGULOS RECTÁNGULOS UTILIZANDO VIDEOJUEGO DISEÑADO POR ESTUDIANTES DE LA I.E HÉCTOR ABAD GÓMEZ.
RECONOCIMIENTO DE SITUACIONES QUE SE PUEDEN MODELAR POR MEDIO DE FUNCIÓN CUADRÁTICA.
En algún momento habrás escuchado el término de parábola, esta se puede definir como una curva que siempre se está abriendo y cada punto de sus dos paredes está a una misma distancia de un punto o foco. En este documento trabajaremos una función cuya gráfica tiene forma de parábola.
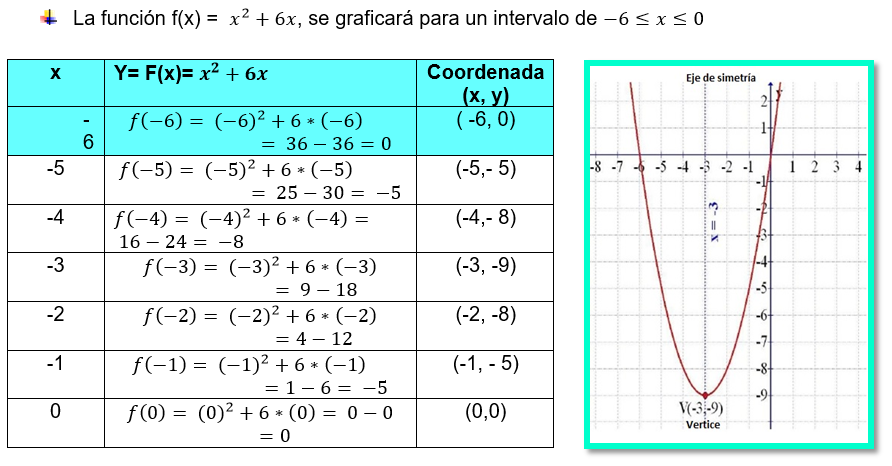
Ejercicio 1
ACTIVIDAD DE PUNTO ADICIONAL
Identifica cuales de las siguientes situaciones de contextos reales describen movimientos parabólicos, marcarlo con una (V ), toma foto y envía al correo de la docente.
ACTIVIDAD DE PUNTO ADICIONAL: reconocimiento de situaciones cotidianas que describen movimientos parabólicos.
ACTIVIDAD DE PUNTO ADICIONAL
Identifica cuales de las siguientes situaciones de contextos reales describen movimientos parabólicos, marcarlo con una (V ), toma foto y envía al correo de la docente.
ACTIVIDAD DE PUNTO ADICIONAL: reconocimiento de situaciones cotidianas que describen movimientos parabólicos.
ALGUNAS DE LAS APLICACIONES EN LA VIDA COTIDIANA DEL CONCEPTO DE FUNCIÓN CUADRÁTICA LA CUAL SE REPRESENTA GRÁFICAMENTE MEDIANTE UNA PARÁBOLA.
ACTIVIDAD #1 : INDAGACIÓN.
FUNCIÓN CUADRÁTICA
Función cuadrática es una función de variable real de la forma :
La representación gráfica de una función cuadrática es la parábola.
Los coeficientes a, b y c, los cuales hacen parte de la función cuadrática son :
a: coeficiente cuadrático ( es el número que acompaña a la variable independiente elevado al cuadrado. Este coeficiente define la concavidad de la parábola que describe la función cuadrática determinada. Si el coeficiente a es positivo la parábola que describe la función es cóncava hacia arriba o convexa. Si el coeficiente a es negativo, la parábola abre hacia abajo, es decir es cóncava hacia abajo o simplemente cóncava.
Ejemplo
b: Coeficiente lineal : Este coeficiente permite determinar si hay o no traslación de la parábola con respecto al eje y. Si el coeficiente b es positivo, la parábola de desplaza hacia el eje negativo de las x, si b = o , la parábola es simétrica con respecto al eje y y si b es negativo la parábola se desplaza hacia el eje de las x positivo.
C: Término independiente: Este valor permite determinar el punto de corte de la función con el eje x, el cual siempre corresponde a un punto de coordenada (0, C).
Ejemplo.
Dada la siguiente función identifica los valores de a, b y c y luego asociarlo con la representación gráfica de la función en el plano cartesiano.
En la función se puede identificar que los coeficientes son:
a: 1, como el coeficiente cuadrático es 1, se puede identificar que la parábola abre hacia arriba por lo tanto es una parábola convexa.
b: - 2 : el valor de b indica que la parábola se traslada hacia el eje positivo de las x.
c: -3, lo que indica que la parábola corta al eje y en un punto de coordenada (0,c) = (0, -3).
2).
En la función 2, se puede identificar que los coeficientes son :
a: , como a es mayor que 0 ( positivo), la parábola abre hacia arriba, por lo tanto es una parábola convexa.
b: 0, el valor de b es cero, debido a que en la función no esta el termino lineal, lo que indica que el valor de b es cero, por tal razón la función es simétrica con respecto al eje y.
c: 1, el valor del coeficiente c es 1, lo que indica que la función corta al eje y en un punto de coordenada (0, 1).
COMPRUEBA SI LO APRENDISTE.
En cada uno de los casos identifica cada uno de los coeficientes de la función cuadrática y construye un esbozo o bosquejo de la representación gráfica de la función en cada uno de los casos.
Enlace : EGOGEBRA PARA GRAFICAR FUNCIONES

ELEMENTOS DE LA PARÁBOLA
En la representación gráfica de una función ( parábola), se pueden identificar los siguientes elementos:
• Concavidad.
• Eje de simetría
• Vértice
• Intercepto o valor de intersección en el eje Y
• Ceros o valores de intersección en el eje X
En la siguiente gráfica puedes identificar cada uno de los elementos de la parábola.
PRUEBA SI LO APRENDISTE
En síntesis, el vértice de la parábola V (x,y), tiene dos componentes de coordenada, una en el eje x y otra en el eje y, las cuales se calculan de la siguiente forma:
• Coordenada del vértice e en el eje x : Xv = - b / 2a
•Componente del vértice en el eje y : Y= f ( -b/2a) o también se puede calcular con la siguiente fórmula:
APLICA LO APRENDIDO
ACTIVIDAD INTERACTIVA DE EJERCITACIÓN SOBRE FUNCIÓN CUADRÁTICA.
Enlace para afianzar tus conocimiento sobre reconocimiento de la expresión algebraica de funciones cuadráticas a partir de su representación gráfica.
El siguiente vídeo te permitirá complementar la información sobre ¿ Cómo calcular las coordenadas del vértice de una parábola a partir de la expresión algebraica que la representa.
El siguiente vídeo te permite complementar la información sobre el calculo de los puntos de corte o de intersección con los eje X y Y.
El siguiente vídeo te perite complementar la información sobre como graficar funciones cuadráticas.
MÁS SOBRE ALGUNOS CAMPOS DE APLICACIÓN DE LA PARÁBOLA.
EJEMPLOS DE SOLUCIÓN DE PROBLEMAS APLICANDO EL CONCEPTO DE FUNCIÓN CUADRÁTICA.
Los siguientes vídeos muestran aplicaciones del concepto de función cuadrática en la solución de situaciones en contextos reales.
Vídeo 1: aplicación de la parábola en la solución de problemas.
Vídeo 2 : aplicación de la parábola en la solución de problemas.
Vídeo 3 : aplicación de la parábola en la solución de problemas.

RECONOZCO SITUACIONES DE MI COTIDIANIDAD RELACIONADAS CON EL CONCEPTO DE FUNCIÓN.
Te invito a activar tus conocimientos haciendo uso del siguiente enlace.
El siguiente vídeo te permitirá construir una definición de función de primer grado.

Imagen tomada de: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEis6XItBwwRTnY70DTEVW6TDXSL4JCB4SFiyoZUEvEA_vdsG3R3geTMgR5l25weImdJT0KGkatCBsXc1qjAbPiksz19vqebN2k34tFW28mxnqE1ldI9fvMeVutFeqfBnPMuQpY3KQLZ_nKY/s320/func_2.jpg
El siguiente vídeo te permitirá establecer diferencias y similitudes entre las funciones de primer grado de tipo lineal y del tipo afín.
FUNCIONES DE PRIMER GRADO DE TIPO LINEALLINEALES
la siguiente actividad te permite colocar a prueba tus conocimientos sobre función de primer grado.
El siguiente vídeo te muestra un problema de aplicación de la función de primer grado de tipo lineal.
CONSTRUCCIÓN DE LA TABLA DE VALORES Y REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN DE PRIMER GRADO DE TIPO LINEAL f(x) = mx
El siguiente vídeo te muestra como construir la tabla de valores de una función de tipo lineal y su representación gráfica.
El siguiente vídeo te permite modelar situaciones en contextos reales donde se aplica la función de tipo lineal.
FUNCIÓN DE PRIMER GRADO DE TIPO AFÍN.
El siguiente enlace te permite ejercitar tus conocimientos sobre funciones de primer grado.
GANA NOTA DE PARTICIPACIÓN DESARROLLANDO EL SIGUIENTE CRUCIGRAMA SOBRE FUNCIÓN DE PRIMER GRADO.
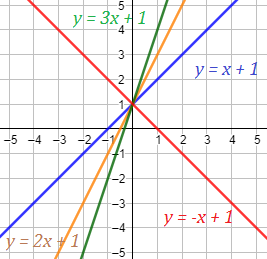
La siguiente gráfica te muestra la representación gráfica de función afín, donde se evidencia el punto de corte con el eje y ( n) y la pendiente m.
EL SIGUIENTE TE PERMITE PODER COMPLEMENTAR LA INFORMACIÓN SOBRE FUNCIÓN LINEAL Y AFÍN.
ACTIVIDAD GANA UN PUNTO ADICIONAL SOBRE TU ACTIVIDAD : GANA UN PUNTO ADICIONAL SOBRE LA NOTA DE TU GUÍA O ACUMULA UN PUNTO EN CUALQUIER ACTIVIDAD REALIZADA
RECONOCE Y MODELA SITUACIONES DE LA VIDA COTIDIANA UTILIZANDO EL CONCEPTO DE FUNCIÓN DE PRIMER GRADO.
CONSTRUCCIÓN DE TABLA DE VALORES Y REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN DE TIPO AFÍN ( f(x)= mx+n)
Los siguientes vídeos te permitirán complementar la información sobre como construir la tabla de valores y la representación gráfica en le plano cartesiano de funciones del tipo afín.
PENDIENTE DE LA RECTA .
CALCULO DE LA PENDIENTE DE UNA RECTA.
El siguiente vídeo te permite familiarizarte con la expresión que permite calcula la pendiente y la clasificación de recta según el valor de la pendiente.
Ejemplo del calculo de la pendiente conocidos dos puntos sobre la recta.
El siguiente vídeo te permite complementar la información sobre la aplicación del concepto de funciones ( lineales y afín ) en la solución e situaciones en contextos reales.
El siguiente vídeo te permite evidenciar los conceptos vistos en el campo de la economía
EL SIGUIENTE ENLACE TE PERMITE COMPLEMENTAR TUS CONOCIMIENTOS SOBRE FUNCIÓN LINEAL, AFÍN, COMO GRAFICAR Y ADEMÁS COMO UTILIZARLAS PARA MODELAR SITUACIONES DE LA VIDA COTIDIANA
ENLACE FUNCIÓN LINEAL Y AFÍN ( REPRESENTACIÓN, GRAFICACIÓN Y APLICACIÓN EN LA SOLUCIÓN DE PROBLEMAS)
AL FINAL DE LA TEMÁTICA SOBRE FUNCIONES DE PRIMER GRADO ( FUNCIÓN LINEAL Y FUNCIÓN AFÍN) TE INVITO A COLOCAR A PRUEBA TUS CONOCIMIENTOS Y GANAR PUNTOS ADICIONALES CON KAHOOT DE MANERA DIVERTIDA.


SISTEMA DE ECUACIONES LINEALES 2X2
El siguiente enlace te permite activar tus conocimientos previos sobre ecuación lineal, el cual se requiere tener presente al momento de resolver sistemas de ecuaciones.
El siguiente vídeo te ilustra sobre el concepto de sistema de ecuación lineal con dos incógnitas.
En el siguiente enlace accederás a un lugar interesante donde te darán a conocer caracteristicas de un sistema de ecuación lineal 2x2 y te ilustrarán sobre los diferentes métodos de resolución.
El siguiente enlace te permitirá conocer las diferentes particularidades de los diferentes métodos de resolución de sistema de resolución de ecuaciones 2x2.
MÉTODOS DE SOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES 2X2.
para resolver sistemas de ecuaciones lineales 2x2, existen varios métodos, entren los que tenemos: reducción, igualación, sustitución, gráfico y por determinante. En este blog abordaremos tres de los cinco métodos enunciados.
SOLUCIÓN DE SISTEMAS DE ECUACIONES 2X2 POR EL MÉTODO DE REDUCCIÓN O ELIMINACIÓN.
ECUACIONES LINEALES
El siguiente vídeo te facilitará el activar tus conceptos previos sobre ecuación lineal.
El siguiente vídeo te ilustra sobre que es la ecuaciones lineales y cuál es su importancia en contextos reales.
UTILIDAD DE LAS ECUACIONES EN LA VÍDA COTIDIANA.
El siguiente vídeo te ilustra sobre algunas de las situaciones en contextos reales donde se aplican las ecuaciones .
El siguiente vídeo te proporciona información sobre diferentes tipos de ecuaciones según el número de exponente o el rol de la incógnita en la expresión algebraicas.
ACTIVIDAD INTERACTIVA SOBRE RECONOCIMIENTO DE ECUACIONES
En el siguiente enlace encontrarás un crucigrama que te permite de manera divertida reconocer ecuaciones, los diferentes tipos de ecuaciones.
traducción del lenguaje común al lenguaje algebraicos.
Las ecuaciones son una herramienta importante para modelar situaciones, interpretar y resolver situaciones en contextos reales. Para esto es muy importante establecer relación entre el lenguaje común y el lenguaje algebraico. El siguiente vídeo te ilustrará sobre cómo modelar situaciones del lenguaje común al lenguaje algebraico.
En el siguiente vídeo se muestra modelación de situaciones mediante ecuaciones lineales.
EL SIGUIENTE ENLACE TE PERMITE ACCEDER A ACTIVIDAD INTERACTIVA DE MODELACIÓN DE SITUACIONES .
En el siguiente enlace encontrará un documento sobre modelación y resolución de situaciones cotidiana mediante ecuaciones
Para facilitar la comprensión del concepto de igualdad el cual es vital al momento de resolver ecuaciones, te invito a que mediante actividad interactiva con balanzas comprendas con facilidad la resolución de ecuaciones.
resolución de ecuaciones lineales con una incógnita
Para resolver ecuaciones con una incógnita, es importante tener en cuenta algunos pasos básicos.
1.
Si
la ecuación lineal tiene signos de agrupación, primero se resuelven las
operaciones planteadas en los signos de agrupación.
2.
Transponer
los términos semejantes a cada lado del igual.
3.
Agrupar
términos semejantes a cada lado del igual (sumar o restar como corresponda).
4.
Despejar
la incógnita (dejarla sola a un lado del igual).
5.
Comprobar
que la solución obtenida sea la correcta.
RESOLUCIÓN DE ECUACIONES CON ENTEROS
El siguiente vídeo te ilustra sobre cómo plantear y resolver ecuaciones lineales con enteros.
En la siguiente tabla se muestra la resolución de ecuaciones lineales con enteros y el procedimiento aplicado.
El siguiente enlace contienen actividad interactiva que te permite repasar la solución de ecuaciones paso a paso.
RESOLUCIÓN DE ECUACIONES CON RACIONEALES.
El siguiente vídeo te muestra cómo resolver ecuaciones con fracciones convirtiéndola en ecuación con enteros .
ACTIVIDAD INTERACTIVA PARA PRACTICAR COLOCAR A PRUEBA TUS CONOCIMIENTOS SOBRE ECUACIONES LINEALES CON ENTEROS .
ECUACIONES LINEALES CON SIGNOS DE AGRUPACIÓN
son expresiones algebraicas que incluyen una igualdad, que tienen una incógnita de exponente 1, y además incluyen signos de agrupación como paréntesis, llaves y corchetes.
Ejemplo de este tipo de ecuaciones:
- 4 ( 3x +2) -18 +2x +16 = 54 -3( x - 4) + 8
- 3 [ 5 (x +1 ) -2 ] +7 = 5 ( 6- 4x)
El siguiente vídeo te ilustra sobre cómo resolver ecuaciones lineales con signos de agrupación.
En la siguiente tabla se muestra un ejemplo sobre la resolución de ecuaciones con signos de agrupación.
ACTIVIDAD INTERACTIVA PARA COLOCAR EN PRACTICA LA RESOLUCIÓN DE ECUACIONES CON SIGNOS DE AGRUPACIÓN.
LE SIGUIENTE ENLACE TE PERMITE COLOCAR A PRUEBA TUS CONOCIMIENTOS SOBRE ECUACIONES LINEALES.
Actividad de punto adicional sobre la resolución de ecuaciones lineales
APLICACIÓN DE ECUACIONES EN LASOLUCIÓN DE PROBLEMAS
Información tomada de : https://redes.colombiaaprende.edu.co/ntg/men/archivos/Referentes_Calidad/Modelos_Flexibles/Postprimaria/Guias%20del%20estudiante/Matematicas/MT_Grado9.pdf
Los siguientes vídeos te complementarán sobre la aplicación de ecuaciones lineales en la solución de problemas.
Vídeo 1
Actividad de participación con punto sobre resolución de problemas aplicando el concepto de ecuaciones lineales.
ECUACIÓN CUADRÁTICA
El siguiente vídeo te muestra la definición, reconocimiento de los elementos de la ecuación cuadrática.
ACTIVIDAD INTERACTIVA DE RECONOCIMIENTO DE ECUACIONES CUADRÁTICAS Y SUS COEFICIENTES.
En el siguiente enlace encuentras actividad interactiva que te permite afianzar tus conocimientos sobre el reconocimiento de ecuaciones cuadráticas y sus diferentes coeficientes (a,b y c).
El siguiente vídeo permite modelar situaciones cotidianas utilizando ecuaciones cuadráticas.
ACTIVIDAD INTERACTIVA DE RECONOCIMIENTO DE ECUACIONES CUADRATICAS
RESOLUCIÓN DE ECUACIONES CUADRÁTICAS.
Las ecuaciones cuadráticas se pueden resolver aplicando varios métodos, entre los que tenemos: factorización y la fórmula general. En este blog ilustraremos la forma de resolver ecuaciones cuadráticas utilizando la fórmula general.
RESOLUCIÓN DE ECUACIONES CUADRÁTICAS UTILIZANDO LA FÓRMULAGENERAL.
El siguiente vídeo te explicará cómo resolver ecuaciones cuadráticas utilizando la fórmula general.
El siguiente vídeo te muestra cómo resolver ecuaciones cuadrática con la fórmula general, teniendo en cuenta los pasos anteriormente dados.
ACTIVIDAD INTERACTIVA SOBRE RESOLUCIÓN DE ECUACIONES CUADRÁTICAS CON LA FORMULA CUADRÁTICA MOSTRANDO PASO A PASO.
En el siguiente enlace encontrarás una actividad interactiva que te permite resolver ecuaciones cuadráticas utilizando la fórmula cuadrática.
Los siguientes vídeos complementará la información sobre resolución de ecuaciones con la solución de problemas.
TABLA DE FRECUENCIA
Los siguientes vídeos te ilustran sobre la construcción de tabla de frecuencia.
El siguiente vídeo te explica sobre tablas de frecuencia y cada uno de los elementos que se encuentran en una tabla de frecuencia.
Vídeos tabla de frecuencia con variable cualitativa
Table de frecuencia variable cuantitativa
El siguiente vídeo te ilustra sobre cómo completar los datos en una tabla de frecuencia cuando se conocen algunos datos y luego realizar un diagrama de barra.
CONJUNTOS NÚMERICO
El siguiente vídeo te ilustrará sobre cómo surgen los conjuntos numéricos, algunos de los conjuntos numéricos que existen , te permiten establecer relación entre los conjuntos numéricos e identificar los elementos que conforma a cada uno de estos y conocer algunos contextos donde tienen aplicación .
CONJUNTO DE LOS NÚMEROS NATURALES
El conjunto de los números naturales es le primer conjunto numérico que surgió, te invito a mirar el siguiente vídeo el cual te ilustrará sobre los números naturales.
conjunto de los números enteros
El siguiente vídeo te ilustra sobre diferentes contextos donde se aplican los números enteros.
El siguiente vídeo te ilustrará sobre el conjunto de los números enteros, los elementos que lo conforman, su representación en le resta y contextos donde estos se aplican.
El siguiente vídeo te ilustrará sobre los números enteros , sus operaciones y propiedades .
CONJUNTO DE LOS NÚMEROS RACIONALES
El siguiente vídeo te ilustra sobre el conjunto de los números racional y los diferentes elementos o tipos de números que pertenecen a este conjunto.
El siguiente vídeo te ilustrará sobre algunos números que hacen parte del conjunto de los números racionales .
REPRESENTACIÓN DE LOS NÚMEROS RACIONALES EN LA RECTA NUMÉRICA
El conjunto de los números racionales es un conjunto diverso, de el hace parte los números enteros ( este incluye a los naturales), las fracciones, los porcentajes, y los números decimales ( exactos, decimales infinitos periódicos). En los siguientes vídeos te mostraremos como ubicar números racionales en forma de fracción y en forma decimal en la recta numérica.
El siguiente vídeo te ilustrará cómo representar racionales en forma de fracción en la recta numérica
El siguiente vídeo te ilustrará sobre cómo representar un número decimal en la recta numérica.
CONJUNTO DE LOS NÚMEROS IRRACIONALES.
El siguiente vídeo te ilustrará sobre el conjunto de los números irracionales y sus características.
CONJUNTO DE LOS NÚMEROS REALES
El siguiente vídeo te ilustrará sobre los números reales y los elementos que los conforman.
ACTIVIDAD INTERACTIVA PARA AFIANZAR EL CONCEPTO DE CONJUNTOS NUMÉRICOS
OPERACIONES CON NÚMEROS REALES EN FORMA DE FRACCIÓN
SUMA Y RESTA DE NÚMEROS REALES
Al sumar o restar números reales, esta puede ser con igual denominador o con diferentes denominadores.
Suma y resta de funciones con igual denominador.
El siguiente vídeo te ilustra sobre suma y resta de reales con forma de fracciones.
coloca en practica tus conocimientos sobre suma y resta de reales en forma de fracción con igual denominador
El siguiente vídeo te ilustra en cómo aplicar suma y resta de reales en forma de fracciones en la solución de problemas.
SUMA Y RESTA DE REALES EN FORMA DE FRACCIÓN.
El siguiente vídeo te ilustra sobre cómo sumar y restar reales en forma de fracción con diferentes denominadores.
El siguiente vídeo te permite complementar el procedimiento sobre suma o resta de varias fracciones.
APLICACIÓN DE SUMA Y RESTA DE REALES EN FORMA DE FRACCIÓN CON DIFERENTES DENOMINADORES
Vídeo 1
ENLACE PARA PRACTICAR SUMA Y RESTA DE FRACCIONES CON DIFERENTES DENOMINADORES .
MULTIPLICACIÓN DE REALES EN FORMA DE GRACCIÓN.
El siguiente vídeo te ilustra sobre cómo multiplicar números reales en forma de fracción.
El siguiente vídeo te ilustra sobre como multiplicar enteros por fracciones.
El siguiente vídeo te ilustrará sobre como multiplicar fracciones por un número decimal
APLICACIÓN DE MULTIPLICACIÓN CON NÚMEROS REALES CON FORMA DE FRACCIÓN EN LA SOLUCIÓN DE PROBLEMAS.
El siguiente vídeo te complementa sobre como utilizar el concepto de multiplicación de fracción en la solución de problemas.
EL SIGUIENTE ENLACE TE PERMITE PRACTICAR TUS CONOCIMIENTOS SOBRE MULTIPLICACIÓN DE FRACCIONES.
actividad interactiva de puntos extras sobre operaciones con reales en forma de fracciones ( suma, resta y multiplicación)
CALCULO DE PORCENTAJE UTILIZANDO REGLA DE TRES
¿QUÉ ES PORCENTAJES ?
El siguiente vídeo te ilustra sobre porcentaje y las diferentes forma de representar un porcentaje.
¿Cómo calcula porcentajes de una cantidad?
El siguiente vídeo te ilustra sobre la aplicación de porcentaje
en la solución de problemas.
te invito a practicar sobre el calculo de porcentajes
actividad de puntos extra sobre porcentajes
DIVISIÓN DE REALES EN FORMA DE FRACCIÓN
El siguiente vídeo te ilustra sobre cómo resolver división de reales en forma de fracciones.
El siguiente vídeo te permite complementar la información sobre división entre tres fracciones .
APLICACIÓN DE DIVISIÓN DE REALES EN FORMA DE FRACCIONES EN LA SOLUCIÓN DE PROBLEMA
El siguiente vídeo te ilustra sobre cómo aplicar el concepto de división de fracciones en la solución de problemas.
ACTIVIDAD PARA COLOCAR A PRUEBA TUS CONOCIMIENTOS SOBRE DIVISIÓN DE FRACCIONES .
OPERACIONES COMBINADAS CON FRACCIONES
El siguiente vídeo te ilustra sobre cómo resolver polinomios con operaciones combinadas con fracciones.
El siguiente vídeo te permite complementar la información sobre resolución de polinomio con signos de agrupación y operaciones combinadas con fracciones.
coloca a prueba tus conocimientos sobre operaciones con reales en forma de fracciones
GRÁFICOS ESTADÍSTICOS
El siguiente vídeo te ilustrará sobre algunos gráfico estadísticos.
El siguiente vídeo te permite complementar la información sobre el calculo de porcentajes a partir de un gráfico de barra.
DIAGRAMA CIRCULAR
El siguiente vídeo te ilustra sobre diagrama circular y como construirlo.
El siguiente vídeo te brinda información sobre cómo medir ángulos.
En el siguiente enlace encuentras una actividad interactiva que te facilita la medición de ángulos, anímate y practica.
El siguiente vídeo te permite complementa la información sobre representación de información mediante un diagrama de barra
ACTIVIDAD DE PUNTO EXTRA SOBRE GRÁFICOS ESTADÍSTICOS
FUNCIÓN ALGEBRAICA
Observa el siguiente vídeo el cual te facilitará construir el concepto de función.
Si una función se puede entender como una máquina, en la cual se ingresa un valor ( variable independiente - dominio), la función le aplica una transformación y arroja como resultado otro valor ( variable dependiente y o f(x)), este permite determinar el rango de la función. Te invito a descubrir cual es la función o transformación que la maquina aplica al valor que ingresa (x) para que se obtenga el valor que sale y 0 f(x). Te invito a mirar el siguiente vídeo para resolver el siguiente reto.
APLICACIÓNES DE FUNCIONES EN LA COTIDIANIDAD
El siguiente vídeo te ilustra sobre algunos contextos reales donde las funciones tienen aplicación.
Te invito a mirar el siguiente vídeo sobre lenguaje algebraico, lo cual te facilitará el planteamiento de funciones de manera algebraica a partir de una situación planteada.
El siguiente vídeo te permite complementar la información sobre la representación algebraica de una función.
TABLA DE VALORES DE UNA FUNCIÓN ALGEBRAICA
COLOCA A PRUEBA TUS CONOCIMIENTOS SOBRE FUNCIONES Y SU REPRESENTACIÓN.
REPRESENTACIÓN DE PUNTOS EN EL PLANO CARTESIANO
Antes de abordar la representación gráfica de funciones en el plano cartesiano te invito a mirar el siguiente vídeo sobre el plano cartesiano y cómo ubicar coordenada en este.
El siguiente vídeo te ilustra sobre la ubicación de puntos en el plano cartesiano.
El siguiente enlace te permite practicar sobre la ubicación de puntos en el plano cartesiano y verificar si lo aprendiste bien.
REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN ALGEBRAICA.
El siguiente vídeo te ilustra sobre cómo construir la representación gráfica de una función.
Vídeo 1: gráfica de función de primer grado
Vídeo 2: Gráfica de una función cuadrática
REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN EN EL PLANO CARTESIANO
Los siguientes vídeos te ilustran sobre la aplicación de funciones algebraicas en la solución de problemas.
Vídeo 1.
Vídeo 2.
El siguiente enlace encuentras el programa llamado Geogebra te ayudará a representar gráficamente funciones.
Practica sobre la representación gráfica de funciones
CÁLCULO DE DISTANCIAS EN EL PLANO CARTESIANO
Los siguientes vídeos te permitirán comprender con facilidad el calculo de distancia en el plano cartesiano.
Vídeo sobre el teorema de Pitágoras
El siguiente Vídeo te permite complementar la información sobre cálculo de distancia en el plano cartesiano.
El siguiente vídeo te permite visualizar diferentes ejemplos sobre el calculo de distancia en el plano cartesiano.















































































































































































No hay comentarios:
Publicar un comentario